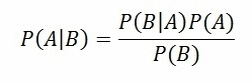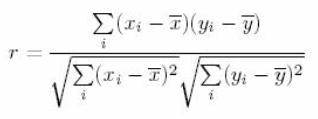MarkLogic Server 11.0 Product DocumentationApplication Developer's Guide — Chapter 20
Machine Learning with the ONNX API
This chapter contains the following sections:
- Overview of Machine Learning
- Terms
- Types of Machine Learning
- Why Using ONNX Runtime in MarkLogic Makes Sense
- Capabilities of the ONNX Runtime
- ONNX XQuery and JavaScript API
- Example ONNX Applications
Overview of Machine Learning
The MarkLogic approach to machine learning is to accelerate and improve the data curation life cycle by developing models using high quality data. Bad inputs result in bad outputs (garbage in = garbage out). In the case of machine learning, the model used to convert input to output is written by the machine itself during training, and that is based on the training input. Bad training data can damage the model in ways you cannot understand, rendering it useless. Because the models are opaque, you may not even know they are damaged. You don't use machine learning to solve easy problems and hard questions answered wrong are hard to identify. MarkLogic has many features, such as the Data Hub Framework and Entity Services, you can leverage to ensure the quality of the data used to create your models.
Machine learning can be conveniently perceived as a function approximator. There is an indescribable law that determines if a picture is a picture of a cat, or if the price of a stock will go up tomorrow, and machine learning can approximate that law (with various degrees of accuracy). The law itself is a black box that takes input and produces output. For image classification, the input is pixel values and the output is cat or not; for a stock price, the input is stock trades and the output is price. A machine learning model takes input in a form understandable by the machine (high dimensional matrix of numbers, called tensors), performs a series of computation on the input, and then produces an output. The machine learns from comparing its output to the ground truth (the output of that law), and adjust its computations of the input, to produce better output that is closer to the ground truth.
Consider again the example of image classification. A simple machine learning model can be like this: convert the image into a matrix of pixel values x; multiply it with another matrix W. If the result Wx is larger than a Threshold, it's a cat, otherwise it's not. For the model to succeed, it needs labeled training data of images. The model starts with a totally random matrix W, and produces output on all training images. It will make lots of mistakes, and for every mistake it makes, it adjusts W so that the output Wx is closer to the ground truth label. The precise amount of adjustment of W is determined through a process called error back propagation. In the example described here, the computation is a simple one matrix multiplication; however, in real world applications, you can have hundreds of layers of computations, with millions of different W parameters.
Terms
The material in this guide assumes you are familiar with the basic concepts of machine learning. Some terms have ambiguous popular definitions, so they are described below.
| Term | Definition |
|---|---|
| Artificial Intelligence | Any technique which enables computers to mimic human behavior |
| Machine Learning | Subset of AI techniques which use mathematical methods (commonly statistics or liner algebra) to modify behavior with execution. |
| Deep Learning | Subset of Machine Learning which makes the computation of neural networks feasible. Deep Learning is associated with a machine learning algorithm (Artificial Neural Network, ANN) which uses the concept of human brain to facilitate the modeling of arbitrary functions. ANN requires a vast amount of data and this algorithm is highly flexible when it comes to model multiple outputs simultaneously. To understand ANN in detail, see https://www.analyticsvidhya.com/blog/2014/10/ann-work-simplified/. |
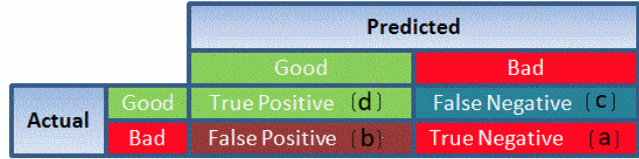
| Accuracy | Accuracy is a metric by which one can examine how good is the machine learning model. Let us look at the confusion matrix to understand it in a better way: So, the accuracy is the ratio of correctly predicted classes to the total classes predicted. Here, the accuracy will be: True Positive + True Negatives __________________________________________________________________ True Positive + True Negatives + False Positives + False Negatives |
| Autoregression | Autoregression is a time series model that uses observations from previous time steps as input to a regression equation to predict the value at the next time step. The autoregressive model specifies that the output variable depends linearly on its own previous values. In this technique input variables are taken as observations at previous time steps, called lag variables. For example, we can predict the value for the next time step (t+1) given the observations at the last two time steps (t-1 and t-2). As a regression model, this would look as follows: X(t+1) = b0 + b1*X(t-1) + b2*X(t-2) Since the regression model uses data from the same input variable at previous time steps, it is referred to as an autoregression. |
| Back Propagation | In neural networks, if the estimated output is far away from the actual output (high error), we update the biases and weights based on the error. This weight and bias updating process is known as Back Propagation. Back-propagation (BP) algorithms work by determining the loss (or error) at the output and then propagating it back into the network. The weights are updated to minimize the error resulting from each neuron. The first step in minimizing the error is to determine the gradient (Derivatives) of each node with respect to the final output. |
| Bayes' Theorem | Bayes' theorem is used to calculate the conditional probability. Conditional probability is the probability of an event 'B' occurring given the related event 'A' has already occurred. For example, a clinic wants to cure cancer of the patients visiting the clinic. The clinic wishes to calculate the proportion of smokers from the ones diagnosed with cancer. Use the Bayes' Theorem (also known as Bayes' rule) as follows: To understand Bayes' Theorem in detail, refer to http://faculty.washington.edu/tamre/BayesTheorem.pdf. |
| Classification Threshold | Classification threshold is the value which is used to classify a new observation as 1 or 0. When we get an output as probabilities and have to classify them into classes, we decide some threshold value and if the probability is above that threshold value we classify it as 1, and 0 otherwise. To find the optimal threshold value, one can plot the AUC-ROC and keep changing the threshold value. The value which will give the maximum AUC will be the optimal threshold value. |
| Clustering | Clustering is an unsupervised learning method used to discover the inherent groupings in the data. For example: Grouping customers on the basis of their purchasing behavior which is further used to segment the customers. And then the companies can use the appropriate marketing tactics to generate more profits. Example of clustering algorithms: K-Means, hierarchical clustering, etc. |
| Confidence Interval | A confidence interval is used to estimate what percent of a population fits a category based on the results from a sample population. For example, if 70 adults own a cell phone in a random sample of 100 adults, we can be fairly confident that the true percentage amongst the population is somewhere between 61% and 79%. For more information, see https://www.analyticsvidhya.com/blog/2015/09/hypothesis-testing-explained/. |
| Convergence | Convergence refers to moving towards union or uniformity. An iterative algorithm is said to converge when as the iterations proceed the output gets closer and closer to a specific value. |
| Correlation | Correlation is the ratio of covariance of two variables to a product of variance (of the variables). It takes a value between +1 and -1. An extreme value on both the side means they are strongly correlated with each other. A value of zero indicates a NIL correlation but not a non-dependence. You'll understand this clearly in one of the following answers. The most widely used correlation coefficient is Pearson Coefficient. Here is the mathematical formula to derive Pearson Coefficient. |
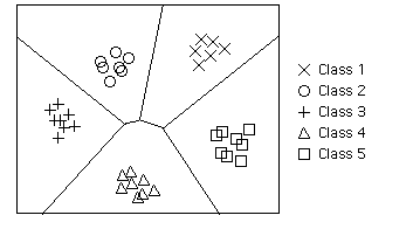
| Decision Boundary | In a statistical-classification problem with two or more classes, a decision boundary or decision surface is a hyper surface that partitions the underlying vector space into two or more sets, one for each class. How well the classifier works depends upon how closely the input patterns to be classified resemble the decision boundary. In the example sketched below, the correspondence is very close, and one can anticipate excellent performance. Here the lines separating each class are decision boundaries. |
| Dimensionality Reduction | Dimensionality Reduction is the process of reducing the number of random variables under consideration by obtaining a set of principal variables. Dimension Reduction refers to the process of converting a set of data having vast dimensions into data with lesser dimensions ensuring that it conveys similar information concisely. Some of the benefits of dimensionality reduction:
|
| Datasets | Training data is used to train a model. It means that ML model sees that data and learns to detect patterns or determine which features are most important during prediction. Validation data is used for tuning model parameters and comparing different models in order to determine the best ones. The validation data must be different from the training data, and must not be used in the training phase. Otherwise, the model would overfit, and poorly generalize to the new (production) data. Test data is used once the final model is chosen to simulate the model's behavior on a completely unseen data, i.e. data points that weren't used in building models or even in deciding which model to choose. |
| Ground Truth | The reality you want your model to predict. |
| Model | A machine-created object that takes input in a form understandable by the machine, performs a series of computation on the input, and then produces an output. The model is built from repeatedly comparing its output to the ground truth and adjusting its computations of the input to produce better output that is closer to the ground truth. |
| Neural Network | Neural Networks is a very wide family of Machine Learning models. The main idea behind them is to mimic the behavior of a human brain when processing data. Just like the networks connecting real neurons in the human brain, artificial neural networks are composed of layers. Each layer is a set of neurons, all of which are responsible for detecting different things. A neural network processes data sequentially, which means that only the first layer is directly connected to the input. All subsequent layers detect features based on the output of a previous layer, which enables the model to learn more and more complex patterns in data as the number of layers increases. When a number of layers increases rapidly, the model is often called a Deep Learning model. It is difficult to determine a specific number of layers above which a network is considered deep, 10 years ago it used to be 3 and now is around 20. There are many types of Neural Networks. A list of the most common can be found https://en.wikipedia.org/wiki/Types_of_artificial_neural_networks. |
| Threshold | A threshold is a numeric value used to determine whether the computed output is a match. Most of the time the value of a threshold is obtained through training. The initial value can be chosen randomly, for example 2.2, then the training algorithm finds out that most of the predictions are wrong (cats classified as dogs), then the training algorithm adjusts the value of the threshold, so that the prediction can be more accurate. Sometimes the threshold is determined manually, like in our current smart mastering implementation. They have a combined score, describing similarity between two entities. If the score is larger than a threshold, the two entities can be considered a match. That threshold is pre-determined, manually. No training is involved. |
Types of Machine Learning
This section describes the types of machine learning:
Supervised Learning
Supervised learning is a family of Machine Learning models that teach themselves by example. This means that data for a supervised ML task needs to be labeled (assigned the right, ground-truth class). For instance, if we would like to build a Machine Learning model for recognizing if a given text is about marketing, we need to provide the model with a set of labeled examples (text + information if it is about marketing or not). Given a new, unseen example, the model predicts its target, such as for the stated example, a label (for example, 1 if a text is about marketing and 0 otherwise).
Unsupervised Learning
Contrary to Supervised Learning, Unsupervised Learning models teach themselves by observation. The data provided to that kind of algorithms is unlabeled (there is no ground truth value given to the algorithm). Unsupervised learning models are able to find the structure or relationships between different inputs. The most important kind of unsupervised learning techniques is clustering. In clustering, given the data, the model creates different clusters of inputs (where similar inputs are in the same clusters) and is able to put any new, previously unseen input in the appropriate cluster.
Reinforcement Learning
Reinforcement Learning (RL) differs in its approach from the approaches we've described earlier. In RL the algorithm plays a game, in which it aims to maximize the reward. The algorithm tries different approaches moves using trial-and-error and sees which one boost the most profit. The most commonly known use cases of RL are teaching a computer to solve a Rubik's Cube or play chess, but there is more to Reinforcement Learning than just games. Recently, there is an increasing number of RL solutions in Real Time Bidding, where the model is responsible for bidding a spot for an ad and its reward is the client's conversion rate.
Why Using ONNX Runtime in MarkLogic Makes Sense
As a MarkLogic developer, there are many advantages to using ONNX for creating Machine Learning applications. For instance:
- Different development teams throughout your enterprise may each use any Machine Learning stack of their choice to create their models. They may then export these models the ONNX format and use them all within a MarkLogic application.
- In some cases, they can use their models as they are, because ONNX currently has native support for PyTorch, CNTK, MXNet, and Caffe2.
- There are also converters available for TensorFlow and CoreML.
- By using ONNX on MarkLogic, your Machine Learning applications are safe from vendor lock-in.
Capabilities of the ONNX Runtime
ONNX stands for Open Neural Network eXchange. As per its official website:
ONNX is an open format to represent deep learning models. With ONNX, AI developers can more easily move models between state-of-the-art tools and choose the combination that is best for them. ONNX is developed and supported by a community of partners.
It is an open source project with an MIT license, with its development led by Microsoft.
A machine learning model can be represented as a computation network, where nodes in the network represent mathematical operations (operators). There are many different machine learning frameworks out there (tensorflow, PyTorch, MXNet, CNTK, etc), all of which have their own representation of a computation network. You cannot simply load a model trained by PyTorch into tensorflow to perform inference. This creates barriers in collaboration. ONNX is designed to solve this problem. Although different frameworks have different representation of a model, they use a very similar set of operators. After all, they are all based on the same mathematical concepts. ONNX supports a wide set of operators, and has both official and unofficial converters for other frameworks. For example, a tensorflow-onnx converter has the ability of taking a tensorflow model, do a traversal of the computation network (it's a just a graph), reconstruct the graph replacing all operators with their ONNX equivalent. Ideally, if all operators supported by tensorflow are also supported by ONNX, we can have a perfect converter, being able to convert any tensorflow model to ONNX format. However this is not the case for most machine learning frameworks. All these frameworks are constantly adding new operators (with some being highly specialized), and it's very hard to keep up with all frameworks. ONNX is under active development, with new operator support added in each release, trying to catch up with the super set of all operators supported by all framework.
ONNX runtime is a high efficiency inference engine for ONNX models. Per its github page :
ONNX Runtime is a performance-focused complete scoring engine for Open Neural Network Exchange (ONNX) models, with an open extensible architecture to continually address the latest developments in AI and Deep Learning. ONNX Runtime stays up to date with the ONNX standard with complete implementation of all ONNX operators, and supports all ONNX releases (1.2+) with both future and backwards compatibility.ONNX runtime's capability can be summarized as:
For (1), ONNX runtime supports loading a model from the filesystem or from a byte array in memory, which is convenient for us; For (2), we need to construct values in CPU memory; For (3), ONNX runtime automatically uses available accelerators and runtimes available on the host machine. An abstraction of a runtime is called an execution provider. Current execution providers include CUDA, TensorRT, Intel MKL, etc. ONNX runtime partitions the computation network (the model) into subgraphs, and run each sub-graph on the most efficient execution provider. A default fallback execution provider (the CPU) is guaranteed able to run all operators, so that even if no special accelerator or runtime (GPU, etc.) exists, ONNX runtime can still perform inference on an ONNX model, albeit at a much slower speed.
Beginning with version 10.0-3, MarkLogic server includes version 1.0.0 of the ONNX runtime.
ONNX XQuery and JavaScript API
The ONNX runtime is under active development, and its C API changes frequently. For this reason, we only provide core functionalities to allow you to achieve all of your objectives with only a minimal knowledge of the C API underneath.
We chose to expose a very small subset of the C API of onnxruntime representing the core functionality. The rest of the C APIs are implemented as options passed to those core APIs.
New Types for the ONNX Runtime
We have introduced two opaque types: ort:session and ort:value. An ort:session represents an inference session based on one loaded model and other options. An ort:value represents an input or output value. ort:values can be used as input values in an inference session, or they can be the return value of a run of an inference session. There are converters between other numeric XQuery data types and ort:value. All options and configurations to ort functions are represented as map:map.
Exposed ONNX Runtime API
All onnxruntime APIs are under the ort namespace. Following is a list of exposed onnxruntime APIs:
| JavaScript | XQuery | Description |
|---|---|---|
| ort.run | ort:run | Perform inference of a session, based on supplied input values. Returns an Object of output names and their values. |
| ort.session | ort:session | Load an ONNX model from the database, as an inference session. The user can then perform runs of this session, with different input values/settings. |
| ort.sessionInputCount | ort:session-input-count | Returns the number of inputs of a session. |
| ort.sessionInputName | ort:session-input-name | Returns the name of an input of a session, specified by an index. |
| ort.sessionInputType | ort:session-input-type | Returns a Map containing the type information of an input of a session, specified by an index |
| ort.sessionOutputCount | ort:session-output-count | Returns the number of outputs of a session. |
| ort.sessionOutputName | ort:session-output-name | Returns the name of an output of a session, specified by an index. |
| ort.sessionOutputType | ort:session-output-type | Returns a Map containing the type information of an output of a session, specified by an index. |
| ort.value | ort:value | Constructs an ort.value to be supplied to an ort.vession to perform inference. |
| ort.valueGetArray | ort:value-get-array | Returns the tensor represented by the ort.value as a flattened one-dimensional Array. |
| ort.valueGetShape | ort:value-get-shape | Returns the shape of the ort.value as an Array. |
| ort.valueGetType | ort:value-get-type | Returns the tensor element type of the ort.value as a String. |
Security
The onnxruntime does not read or write to the database or the file system.
The following functions require special privileges:
These privileges are assigned to the ort-user role. A user must have the ort-user role to execute these functions.
Limitations
We do not support custom operators, due to ONNX runtime listing them as Experimental APIs.
There is no distributed inference in the ONNX runtime. This is partly because an inference session runs relatively fast: the runtime performs just one forward pass of the model, without auto-differential, and with no need for millions of iterations. In addition, multiple inference sessions can be executed under a single ONNX runtime.
Example ONNX Applications
This section describes two example ONNX applications:
Example ONNX Application using JavaScript
Download the ONNX sample model file from the the ONNX Model Zoo page at:
https://s3.amazonaws.com/onnx-model-zoo/squeezenet/squeezenet1.1/squeezenet1.1.onnx
Use the Query Console to load it into the Documents database. This may be run by using the Query Console, select Documents as the Database and JavaScript as the Query Type.
declareUpdate(); xdmp.documentLoad('c:\\temp\\squeezenet1.1.onnx', { uri : '/squeezenet.onnx', permissions : xdmp.defaultPermissions(), format : 'binary' });
Using the Query Console, select Documents as the Database and JavaScript as the Query Type and run the following query to load a model, define some runtime values, and perform an evaluation:
'use strict'; const session = ort.session(cts.doc("/squeezenet.onnx")) const inputCount = ort.sessionInputCount(session) const outputCount = ort.sessionOutputCount(session) var inputNames = [] var i,j for (i=0;i<inputCount;i++){ inputNames.push(ort.sessionInputName(session, i)) } var outputNames = [] for (i=0;i<outputCount;i++){ outputNames.push(ort.sessionOutputName(session, i)) } var inputTypes = [] for (i=0;i<inputCount;i++){ inputTypes.push(ort.sessionInputType(session, i)) } var outputTypes = [] for (i=0;i<outputCount;i++){ outputTypes.push(ort.sessionOutputType(session, i)) } var inputValues = [] for (i=0;i<inputCount;i++){ var p = 1 for(j=0;j<inputTypes[i]["shape"].length;j++){ p *= inputTypes[i]["shape"][j] } var data = [] for(j=0;j<p;j++){ data.push(j); } inputValues.push(ort.value(data, inputTypes[i]["shape"], "float")) } var inputMap = {} for (i=0;i<inputCount;i++){ inputMap[inputNames[i]] = inputValues[i] } ort.run(session, inputMap)
The output will look like the following:
{ "softmaxout_1": "OrtValue(Shape:[1, 1000, 1, 1], Type: FLOAT)" }
Example ONNX Application using XQuery
The following example performs the same actions as the previous example, but in the XQuery language:
xquery version "1.0-ml"; let $session := ort:session(fn:doc("/squeezenet.onnx")) let $input-count := ort:session-input-count($session) let $output-count := ort:session-output-count($session) let $input-names := for $i in (0 to $input-count - 1) return ort:session-input-name($session, $i) let $output-names := for $i in (0 to $output-count - 1) return ort:session-output-name($session, $i) let $input-types := for $i in (0 to $input-count - 1) return ort:session-input-type($session, $i) let $output-types := for $i in (0 to $output-count - 1) return ort:session-output-type($session, $i) let $input-values := for $i in (1 to $input-count) (: generate some arbitrary input data. :) let $data := (1 to fn:fold-left(function($a, $b) { $a * $b }, 1, map:get($input-types, "shape"))) return ort:value($data, map:get($input-types, "shape"), map:get($input-types, "tensor-type")) let $input-map := map:map() let $input-maps := for $i in (1 to $input-count) return map:with($input-map, $input-names[$i], $input-values[$i]) let $input-map := $input-maps[$input-count] return ort:run($session, $input-map)
The output will look like the following:
<map:map xmlns:map="http://marklogic.com/xdmp/map" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xmlns:xs="http://www.w3.org/2001/XMLSchema"> <map:entry key="softmaxout_1"> <map:value xsi:type="ort:value" xmlns:ort="http://marklogic.com/onnxruntime">OrtValue(Shape:[1, 1000, 1, 1], Type: FLOAT)</map:value> </map:entry> </map:map>